Tool to generate permutations of items, the arrangement of distinct items in all possible orders: 123,132,213,231,312,321.
Permutations - dCode
Tag(s) : Combinatorics
dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day!
A suggestion ? a feedback ? a bug ? an idea ? Write to dCode!
Permutations
Permutations Generator
Permutations/Anagrams Calculator
Answers to Questions (FAQ)
What is a permutation? (Definition)
In Mathematics, item permutations consist in the list of all possible arrangements (and ordering) of these elements in any order.
Example: The three letters A,B,C can be shuffled (anagrams) in 6 ways: A,B,C B,A,C C,A,B A,C,B B,C,A C,B,A
Permutations should not be confused with combinations (for which the order has no influence) or with arrangements also called partial permutations (k-permutations of some elements).
How to generate permutations?
The best-known method is the Heap algorithm (method used by this dCode's calculator).
Here is a pseudo code source : function permute(data, n) {
if (n = 1) print data
else {
for (i = 0 .. n-2) {
permute(data, n-1)
if (n % 2) swap(data[0], data[n-1])
else swap(data[i], data[n-1])
permute(data, n-1)
}
}
}
Permutations can thus be represented as a tree of permutations: 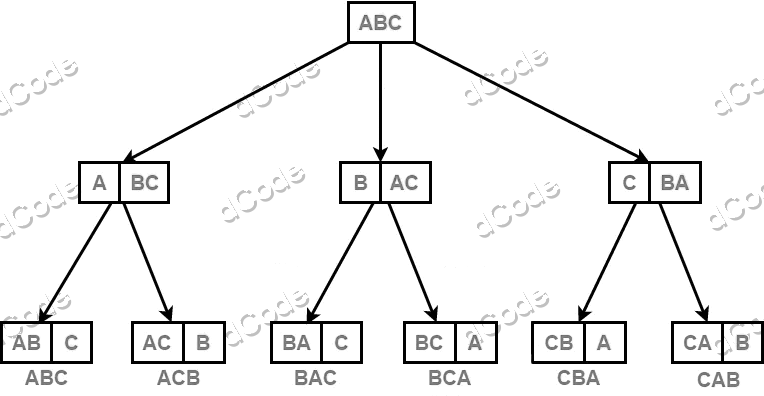
How to count permutations?
Counting permutations uses combinatorics and factorials
Example: For $ n $ items, the number of permutations is equal to $ n! $ (factorial of $ n $)
How to count distinguishable permutations?
Having a repeated item involves a division of the number of permutations by the number of permutations of these repeated items.
Example: DCODE 5 letters have $ 5! = 120 $ permutations but contain the letter D twice (these $ 2 $ letters D have $ 2! $ permutations), so divide the total number of permutations $ 5! $ by $ 2! $: $ 5!/2!=60 $ distinct permutations.
Source code
dCode retains ownership of the "Permutations" source code. Any algorithm for the "Permutations" algorithm, applet or snippet or script (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or any "Permutations" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) or any database download or API access for "Permutations" or any other element are not public (except explicit open source licence like Creative Commons). Same with the download for offline use on PC, mobile, tablet, iPhone or Android app.
Reminder: dCode is an educational and teaching resource, accessible online for free and for everyone.
Cite dCode
The content of the page "Permutations" and its results may be freely copied and reused, including for commercial purposes, provided that dCode.fr is cited as the source.
Exporting the results is free and can be done simply by clicking on the export icons ⤓ (.csv or .txt format) or ⧉ (copy and paste).
To cite dCode.fr on another website, use the link:
In a scientific article or book, the recommended bibliographic citation is: Permutations on dCode.fr [online website], retrieved on 2025-04-15,
