Tool for encryption and decryption of messages using the rotating grid (Fleissner) technique aka Turning Grille. Find out how to secure your communications with this historic cryptographic method.
Turning Grille - dCode
Tag(s) : Transposition Cipher, Grid Cipher
dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day!
A suggestion ? a feedback ? a bug ? an idea ? Write to dCode!
Turning Grille
Turning Grille Decoder
Turning Grille Encoder
Answers to Questions (FAQ)
What is a turning grid cipher? (Definition)
The turning grille, or Fleissner grille, is a transposition cipher. It relies on the use of a windowed grid (a cover filled with holes) placed over an empty matrix. The letters of the message are written in the visible openings. By rotating the cover in a specific order, the remaining spaces are gradually filled until the entire message is concealed within the grid.
How to encrypt using a turning grid?
To encode a message with a rotating grid, the user places a perforated grid or sheet with holes on top of a blank grid.
Example: Encrypt the message FLEISSNERGRILLE with the grid
| ▮ | ▮ | ▮ | ▮ |
| ▮ | ▮ | ▯ | ▯ |
| ▮ | ▮ | ▮ | ▯ |
| ▯ | ▮ | ▮ | ▮ |
The locations visible through the holes are then filled with the letters of the plain message.
Example:
| ▮ | ▮ | ▮ | ▮ |
| ▮ | ▮ | F | L |
| ▮ | ▮ | ▮ | E |
| I | ▮ | ▮ | ▮ |
Once filled, the perforated grid is then turned a quarter turn (clockwise or counterclockwise), revealing new free spaces, which are in turn filled with the letters of the plain message.
Example:
| 1⟳ |
| 2⟳ |
| 3⟳ |
|
After 4 rotations, the grid is supposed to be full.
Reading the letter grid online constitutes the encrypted message.
Example: The message is encrypted SLLRGEFLRISEINEG from the grid obtained:
| S | L | L | R |
| G | E | F | L |
| R | I | S | E |
| I | N | E | G |
If the message contains more letters, then repeat the steps with the following letters and a new blank grid (but keeping the same perforated grid).
If the grid is not completely filled, insert random/neutral letters to fill in the holes.
The grid must respect certain rules so that the holes do not end up on the same letters after rotation.
How to decrypt a message with a turning grid?
To decode a message encrypted with a spinning grid, the player places the perforated grid over the encoded text, aligning the holes with the characters.
The characters visible through the perforation holes reveal the letters of the original message.
After 4 clockwise rotations (or counterclockwise), the original message is completely reconstituted.
If the message contains more letters, then repeat the steps with the following letters.
How to generate a valid grid?
The grid must have 1/4 holes for every 3/4 non-holes. Since the holes successively occupy 4 positions, only one of these positions can contain a hole.
An easy way to avoid having duplicate holes is to separate the grid into 4 quadrants, then number the boxes as follows: 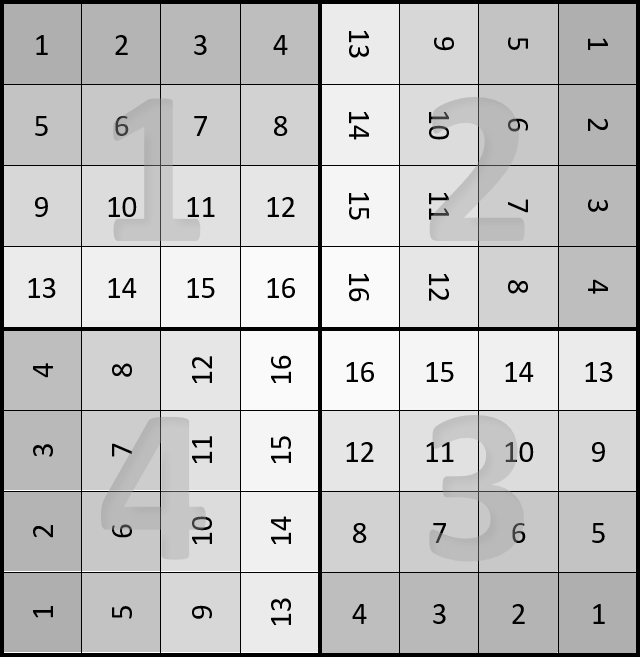
Make holes for each value, but limiting yourself to 1 hole per value (at any random location among the 4).
For odd-sized grids, ignore the central box.
Why are these grids called Fleissner grilles?
The rotating grid method was detailed by the Austrian Colonel Edouard Fleissner von Wostrowitz, who detailed it in his work entitled Handbuch der Kryptographie. Although it cannot be said with certainty that he was the inventor, because encryption techniques using grids had existed for a long time, Fleissner's name remained associated with this method.
Jules Verne, in 1885, incorporated this cryptographic technique into his novel Mathias Sandorf, crediting it to Fleissner.
This type of grilles was used during the First World War by the German army. Each grid size had a code name: Anna 5x5, Berta 6x6, Clara 7x7, Dora 8x8, Emil 9x9, Franz 10x10.
How to recognize a turning grid ciphertext? (Identification)
The encrypted message is a transposition of the letters, the coincidence index is similar to that of the plain text.
The presence of a punched card (or any other similar object) should bring to mind this method or the Cardan cipher.
Any reference to Mathias Sandorf or Jules Verne is a clue.
How to decipher without grid? (Attacks)
Deciphering a message without having the corresponding grid is difficult.
Potential attacks include searching for recurring patterns in the ciphertext, statistical analysis of letters, but especially brute force methods. The number of permutations of the grid is relatively limited if its size is small.
What are the variants of the turning grid cipher?
There are several variations of the rotating grille, including different sized racks or methods of rotating the grille clockwise or counterclockwise.
Source code
dCode retains ownership of the "Turning Grille" source code. Any algorithm for the "Turning Grille" algorithm, applet or snippet or script (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or any "Turning Grille" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) or any database download or API access for "Turning Grille" or any other element are not public (except explicit open source licence). Same with the download for offline use on PC, mobile, tablet, iPhone or Android app.
Reminder: dCode is an educational and teaching resource, accessible online for free and for everyone.
Cite dCode
The content of the page "Turning Grille" and its results may be freely copied and reused, including for commercial purposes, provided that dCode.fr is cited as the source (Creative Commons CC-BY free distribution license).
Exporting the results is free and can be done simply by clicking on the export icons ⤓ (.csv or .txt format) or ⧉ (copy and paste).
To cite dCode.fr on another website, use the link:
In a scientific article or book, the recommended bibliographic citation is: Turning Grille on dCode.fr [online website], retrieved on 2026-01-01,
- Turning Grille Decoder
- Turning Grille Encoder
- What is a turning grid cipher? (Definition)
- How to encrypt using a turning grid?
- How to decrypt a message with a turning grid?
- How to generate a valid grid?
- Why are these grids called Fleissner grilles?
- How to recognize a turning grid ciphertext? (Identification)
- How to decipher without grid? (Attacks)
- What are the variants of the turning grid cipher?
