Coordonnées Antipodales

Deux points sont dits antipodaux s'ils se trouvent à deux points opposés sur un cercle ou une sphère. Ils sont diamétralement opposés, c'est à dire que ce sont les points les plus éloignés l'un de l'autre sur une sphéroïde.

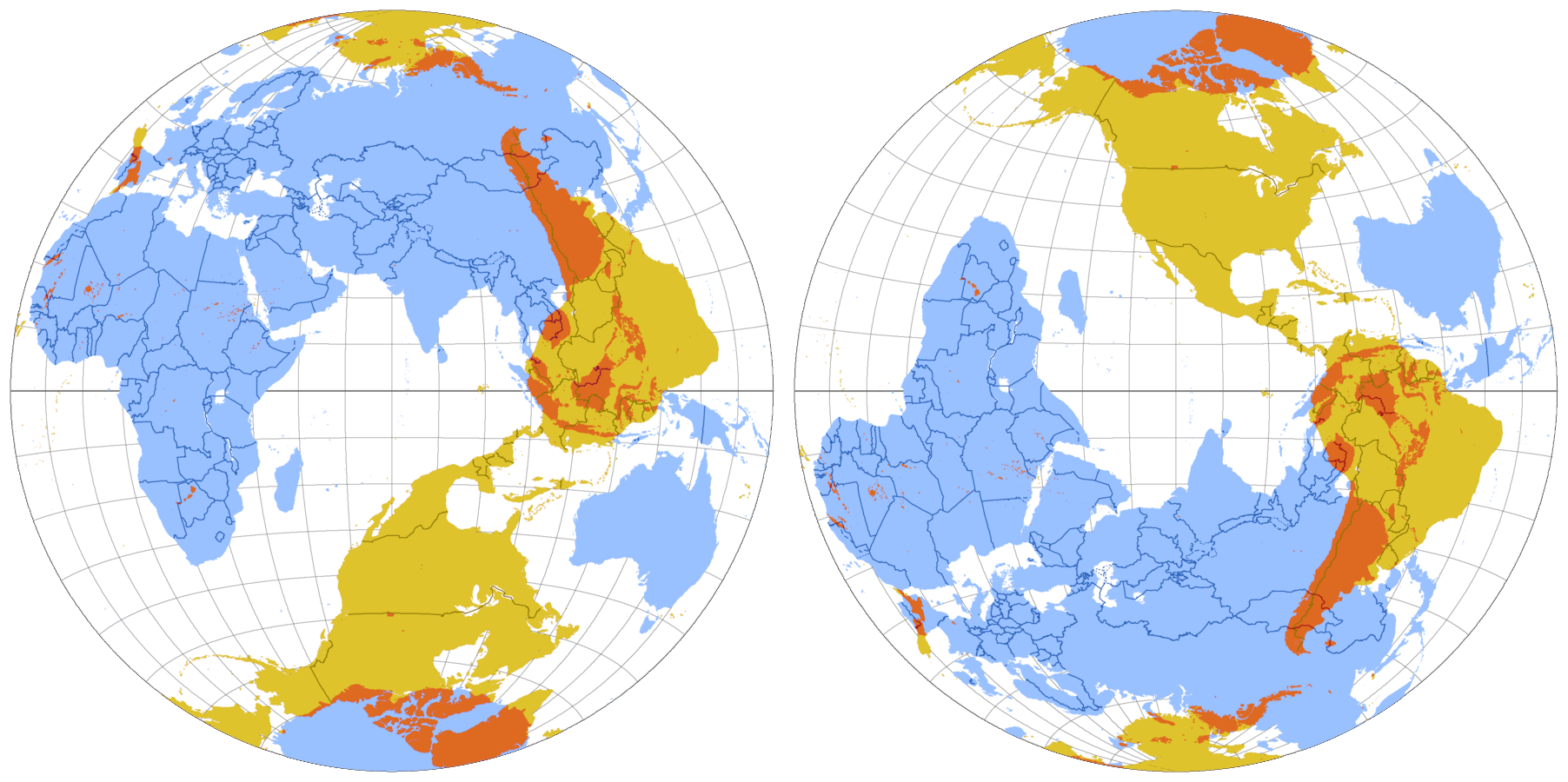
Voici une image présentant le globe terrestre avec les continents présentés une fois en jaune, et une seconde fois en bleu mais avec leurs coordonnées antipodales (source Wikipedia).

Les portions où les continents jaunes et bleus se superposent, sont des emplacements sur Terre, où creuser un trou rectiligne, perpendiculaire au sol et passant par le centre de la terre permettrait d'atterrir sur un autre continent.

— A partir des coordonnées sphérique (sur une sphère), prendre l'opposé de la latitude (ce qui revient à mettre ou enlever un signe moins - devant), et enlever/ajouter 180 à la longitude (afin de la conserver dans l'intervalle [-180;+180] ) pour des coordonnées GPS.

Les coordonnées antipodales $ (\theta', \phi') $ d'un point $ (\theta, \phi) $ sur une sphère sont données par $ \theta' = \theta \pm 180^\circ $ et $ \phi' = -\phi $.

— A partir de coordonnées cartésiennes 3D, prendre l'opposé de chaque composante (x,y,z) soit (-x,-y,-z)

— A partir d'une adresse/ville, utiliser un outil de géocodage (permettant de retrouver les coordonnées GPS d'une adresse).

Les lignes de longitude (verticales) connectent les points antipodaux, suivre une ligne de longitude garanti de passer par le point antipodal autour de la sphère.

Pour sa position, mesurer la distance à un pole du point original, et la reporter sur l'autre pole pour trouver le point antipodal.

Très peu de villes sont aux antipodes l'une de l'autre, mais il y a La Coruña (Espagne) et Christchurch (Nouvelle-Zélande) ou Pékin (Chine) et Bahía Blanca (Argentine) ou encore Taipei (Taiwan) et Asunción (Paraguay)