Tool for calculating logarithms with the logarithm function is denoted log or ln, defined by a base (the base e for the natural logarithm).
Logarithm - dCode
Tag(s) : Functions
dCode is free and its tools are a valuable help in games, maths, geocaching, puzzles and problems to solve every day!
A suggestion ? a feedback ? a bug ? an idea ? Write to dCode!
Logarithm
Logarithm Calculator Log(x)=?
Logarithm Expression Simplifier
Logarithm Solver Log(?)=x
Answers to Questions (FAQ)
What is the natural logarithm? (Definition)
The definition of the natural logarithm is the function whose derivative is the inverse function of $ x \mapsto \frac 1 x $ defined for $ x \in \mathbb{R}_+^* $.
The natural logarithm is noted log or ln and is based on the number $ e \approx 2.71828\ldots $ (see decimals of number e).
Example: $ \log(7) = \ln(7) \approx 1.94591 $
Some people and bad calculators use $ \log $ for $ \log_{10} $, so make sure to know which notation is used. The dCode calculator always uses $ \log = \ln $.
How to turn a base N logarithm into a natural logarithm?
Any base $ N $ logarithm can be calculated from a natural logarithm with the formula: $$ \log_{N}(x) = \frac {\ln(x)} {\ln(N)} $$
It follows that $ log_{a}(b) = \frac {\ln(b)} {\ln(a)} $ and $ log_{b}(a) = \frac {\ln(a) } {\ln(b)} $ are inverses
What is the neperian logarithm?
The neperian logarithm is the other name of the natural logarithm (with base e).
What is the decimal logarithm (log10)?
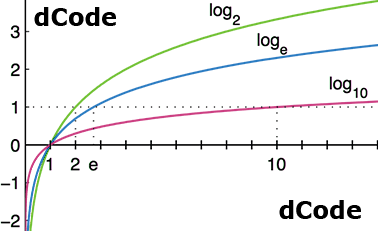
The decimal logarithm noted $ \log_{10} $ or log10 is the base $ 10 $ logarithm. This is one of the most used logarithms in calculations and logarithmic scales. $$ \log_{10}(x) = \frac {\ln(x)} {\ln(10)} $$
Example: $ \log_{10}(1000) = 3 $
What is the binary logarithm (log2)?
The binary logarithm noted $ \log_{2} $ (or sometimes $ lb $) is the base $ 2 $ logarithm. This logarithm is used primarily for computer calculations. $$ \log_2(x) = \frac {\ln(x)} {\ln(2)} $$
Use the formula above to calculate a log2 with a calculator with only the log key.
Why the logarithm can transform product into sum?
Any logarithm has as for properties:
— $ \log_b(x \cdot y) = \log_b(x) +\log_b(y) $ (transformation of a product into a sum)
— $ \log_b \left( \frac{x}{y} \right) = \log_b(x) - \log_b(y) $ (transformation of a quotient into subtraction)
— $ \log_b (x^a) = a \log_b(x) $ (transformation of a power into a multiplication)
What are remarkable values of the logarithm function?
— $ \log_b(b) = 1 $
— $ \log(e) = \ln(e) = 1 $
— $ \log_{10}(10) = 1 $
— $ \log_b(1) = ln(1) = 0 $
— $ \log_b(b^n) = \ln(e^n) = n $ (inverse function of exponentiation)
Source code
dCode retains ownership of the "Logarithm" source code. Any algorithm for the "Logarithm" algorithm, applet or snippet or script (converter, solver, encryption / decryption, encoding / decoding, ciphering / deciphering, breaker, translator), or any "Logarithm" functions (calculate, convert, solve, decrypt / encrypt, decipher / cipher, decode / encode, translate) written in any informatic language (Python, Java, PHP, C#, Javascript, Matlab, etc.) or any database download or API access for "Logarithm" or any other element are not public (except explicit open source licence like Creative Commons). Same with the download for offline use on PC, mobile, tablet, iPhone or Android app.
Reminder: dCode is an educational and teaching resource, accessible online for free and for everyone.
Cite dCode
The content of the page "Logarithm" and its results may be freely copied and reused, including for commercial purposes, provided that dCode.fr is cited as the source.
Exporting the results is free and can be done simply by clicking on the export icons ⤓ (.csv or .txt format) or ⧉ (copy and paste).
To cite dCode.fr on another website, use the link:
In a scientific article or book, the recommended bibliographic citation is: Logarithm on dCode.fr [online website], retrieved on 2025-04-16,
- Logarithm Calculator Log(x)=?
- Logarithm Expression Simplifier
- Logarithm Solver Log(?)=x
- What is the natural logarithm? (Definition)
- How to turn a base N logarithm into a natural logarithm?
- What is the neperian logarithm?
- What is the decimal logarithm (log10)?
- What is the binary logarithm (log2)?
- Why the logarithm can transform product into sum?
- What are remarkable values of the logarithm function?