Outil pour convertir les codes open location en coordonnées GPS sur une carte. Open Location est un système de géocodage créé par Google (parfois renommé 'plus codes') et affiché, entre autres, sur Google Maps.
Open Location (Plus Code) - dCode
Catégorie(s) : Géographie
dCode est gratuit et ses outils sont une aide précieuse dans les jeux, les maths, les énigmes, les géocaches, et les problèmes à résoudre au quotidien !
Une suggestion ? un problème ? une idée ? Écrire à dCode !
Open Location (Plus Code)
Convertisseur de Codes Open Location
Réponses aux Questions (FAQ)
Qu'est ce qu'un code Open Location OLC ? (Définition)
Les codes Open Location (parfois appelés Plus Codes) sont un système de codage de zone géographique sur Terre à la manière de coordonnées GPS. Ils sont pour avantage d'être plus court et concis grâce à un code alphanumérique ce qui les distingue des autres systèmes de coordonnées utilisés en cartographie.
Comment fonctionnent les codes Open Location ?
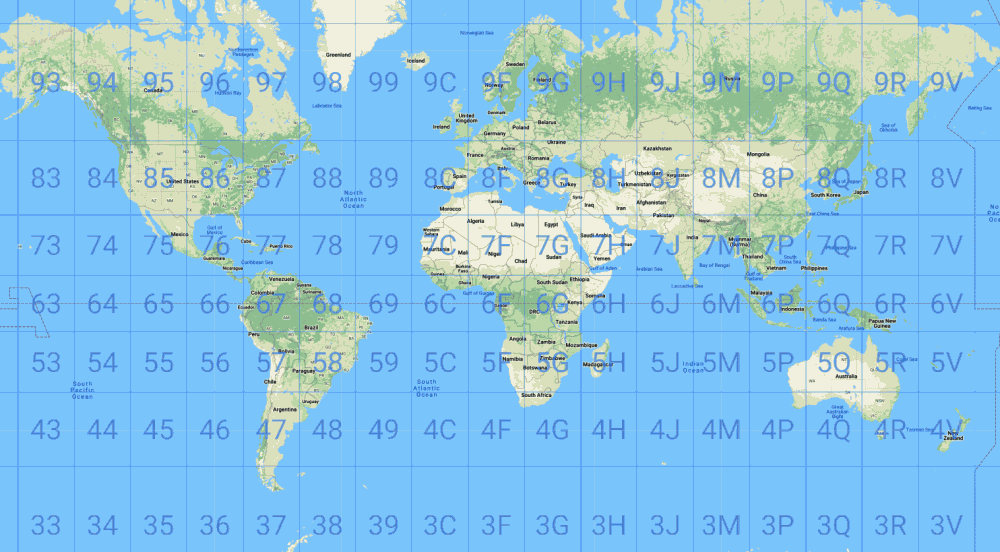
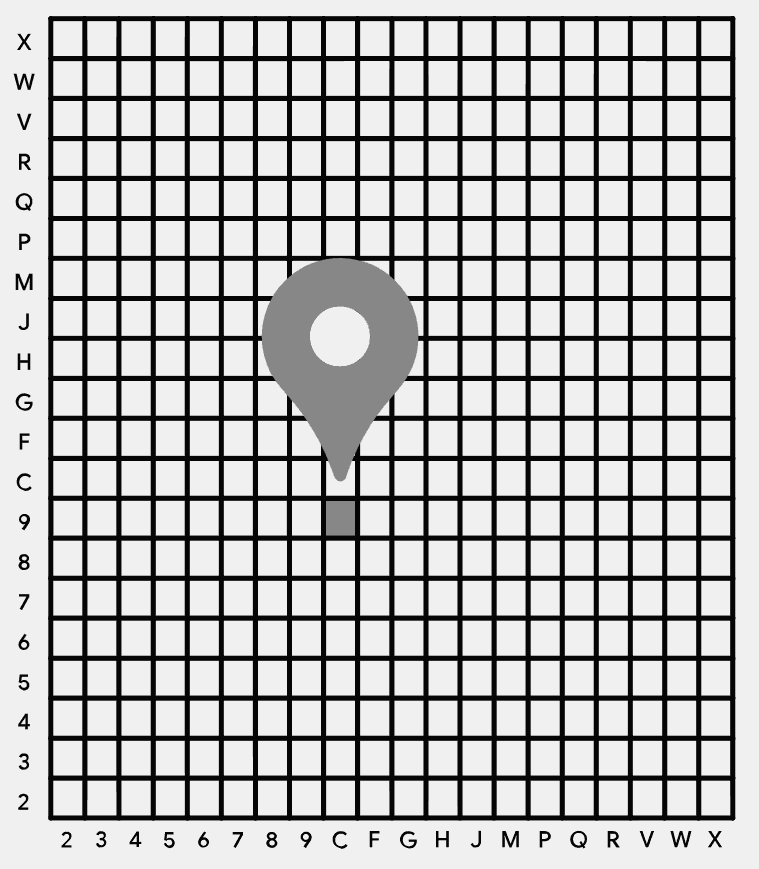
La Terre est d'abord découpée en zones géographiques selon une grille de 18x9 (tous les 20°) et identifiée par 2 caractères (AA), puis chaque zone est découpée en sous-zones (grille de 20x20) identifiées par les sous-coordonnées (BB) etc, elles mêmes redécoupées en 20x20 jusqu'à 4 fois.
Optionnellement, une dernière fois, la zone est découpée en une grille de 4x5 (4 de large, 5 de haut) identifiant 20 cases, numérotées de gauche à droite et de bas en haut, cette dernière zone est la plus précise (3.5m², précision maximale autorisée par le code).
Exemple : AABBCCDD+EEF est un code Open Location complet
Exemple : AABB+CC est un code Open Location court (short code)
Un code est composé de 2 parties séparées par un signe plus + de la forme AABBCCDD+EEF ou encore AABB+CC. La première partie est composée de 1 à 4 couples alphanumériques (BB,CC,DD sont optionnels), la seconde partie est optionnelle également, mais moins il y a de lettres, moins l'emplacement est précis.
Le signe plus est également optionnel, mais il fait partie de la signature du code et le rend plus simple à lire.
Les 20 caractères autorisés pour coder les zones sont 23456789CFGHJMPQRVWX (ils s'utilisent comme une écriture en base 20)
Comment convertir un code Open Location en coordonnées GPS ?
Séparer les couples de caractères et pour chacun, noter le premier caractère (coordonnée de latitude) et le second caractère (coordonnée de longitude) à repérer dans la grille.
Pour reconstituer des coordonnées GPS (latitude, longitude), il est d'abord nécessaire de convertir les caractères 23456789CFGHJMPQRVWX selon le tableau de correspondance :
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | C | F | G | H | J | M | P | Q | R | V | W | X |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
Puis pour chaque valeur, la multiplier par la précision de chaque couple selon le tableau
| #1 AA | 20° |
| #2 BB | 1° |
| #3 CC | 0.05° |
| #4 DD | 0.0025° |
| #5 EE | 0.000125° |
| #6 F | 0.00003125° |
Additionner toutes les valeurs de latitude et y soustraire 90° d'un coté et toutes valeurs de longitude et y soustraire 180° de l'autre pour obtenir des coordonnées GPS.
Exemple : Le code 8FW4V75R+8W se découpe en paires 8F,W4,V7,5R,8W
La première paire 8F consiste en la latitude $ \texttt{8} \rightarrow 6 \times 20° = 120° $ et la longitude $ \texttt{F} \rightarrow 9 \times 20° = 180° $
La seconde paire est W4 donc latitude +18° et longitude +2° etc.
Les sommes respectives donnent la latitude $ \approx 138.8583 - 90 = 48.8583° $ et la longitude $ \approx 182.2923 - 180 = 2.2923° $ soit les coordonnées GPS $ (48.8583, 2.2923) $
Comment convertir des coordonnées GPS en code Open Location ?
A partir de coordonnées GPS :
Exemple : (lat, long) = 48.8583,2.2923
1- ajouter 90° à la latitude et 180° à la longitude
Exemple : $ 48.8583+90=138.8583 $, $ 2.2923+180=182.2923 $
2- multiplier les valeurs par 8000 (=20^3)
Exemple : $ 138.8583 \times 8000 = 1110866.4 $, $ 182.2923 \times 8000 = 1458338.4 $
3- convertir les valeurs obtenues en base 20 (avec l'alphabet 23456789CFGHJMPQRVWX) en se limitant à la partie entière et en complétant avec des zéros initiaux si le résultat a moins de 5 chiffres.
Exemple : $ 1110866_{(10)} = [6, 18, 17, 3, 6]_{(20)} = \texttt{8WV58} $, $ 1458338_{(10)} = [9, 2, 5, 16, 18]_{(20)} = \texttt{F47RW} $
4- intercaler les $ 2 \times 5 $ caractères obtenus en alternant latitude puis longitude et écrire le résultat sous la forme XXXXXXXX+XX
Exemple : 8WV58 et F47RW donnent 8F,W4,V7,5R,8W soit le plus code 8FW4V75R+8W
Comment reconnaitre les codes Open Location ?
Les codes Open Location (OLC) sont au format XXXXXXXX+XX ou parfois XXXX+XX Lieu (les 4 premiers caractères sont supprimés) cette seconde forme nécessite une base de données afin de connaitre le lieu qui permet de retrouver les 4 premiers caractères.
Les codes ont un + d'où leur surnom de plus codes
L'entreprise Google a créé ces codes qui sont de plus en plus utilisés, grace à Google Maps/Earth, toute référence au moteur de recherche est un indice.
Les références aux voyages, voyageurs, tourisme, la Terre, le monde etc. sont des indices.
Où insérer le signe + ?
Le signe plus + n'a pas de fonction codante, il est inutile pour le calcul, mais en pratique, il est positionné 2 caractères avant la fin pour les codes ayant un nombre pair de caractères AABBCCDD+EE ou AABB+CC, ou 3 caractères avant la fin pour les codes ayant un nombre de caractère impair AABBCCDD+EEF.
Comment convertir les plus code en adresse ?
Le passage de coordonnées géographique à une adresse (postale) s'appelle le géocodage. Il est indépendant du format des coordonnées, mais généralement les coordonnées GPS sont préférées pour ce genre de service.
En pratique, pour convertir un plus code, commencer par le transformer en coordonnées GPS, puis utiliser un service de géocodage.
Code source
dCode se réserve la propriété du code source pour "Open Location (Plus Code)". Tout algorithme pour "Open Location (Plus Code)", applet ou snippet ou script (convertisseur, solveur, chiffrement / déchiffrement, encodage / décodage, encryptage / décryptage, traducteur) ou toutes fonctions liées à "Open Location (Plus Code)" (calculer, convertir, résoudre, décrypter / encrypter, déchiffrer / chiffrer, décoder / encoder, traduire) codés en langage informatique (Python, Java, C#, PHP, Javascript, Matlab, etc.) ou toute base de données, ou accès API à "Open Location (Plus Code)" ou tout autre élément ne sont pas publics (sauf licence open source explicite type Creative Commons). Idem avec le téléchargement pour un usage hors ligne sur PC, mobile, tablette, appli iPhone ou Android.
Rappel : dCode est une ressource éducative et pédagogique, accessible en ligne gratuitement et pour tous.
Citation
Le contenu de la page "Open Location (Plus Code)" ainsi que ses résultats peuvent être copiés et réutilisés librement, y compris à des fins commerciales, à condition de mentionner dCode.fr comme source.
L'export des résultats est gratuit et se fait simplement en cliquant sur les icônes d'export ⤓ (format .csv ou .txt) ou ⧉ copier-coller.
Pour citer dCode.fr sur un autre site Internet, utiliser le lien :
Dans un article scientifique ou un livre, la citation bibliographique recommandée est : Open Location (Plus Code) sur dCode.fr [site web en ligne], consulté le 22/04/2025,
- Convertisseur de Codes Open Location
- Qu'est ce qu'un code Open Location OLC ? (Définition)
- Comment fonctionnent les codes Open Location ?
- Comment convertir un code Open Location en coordonnées GPS ?
- Comment convertir des coordonnées GPS en code Open Location ?
- Comment reconnaitre les codes Open Location ?
- Où insérer le signe + ?
- Comment convertir les plus code en adresse ?
