Outil pour le chiffrement et le déchiffrement de messages grâce à la technique de la grille tournante (de Fleissner). Découvrez comment sécuriser vos communications avec cette méthode cryptographique historique.
Grille Tournante - dCode
Catégorie(s) : Chiffrement par Transposition, GRID_CIPHER
dCode est gratuit et ses outils sont une aide précieuse dans les jeux, les maths, les énigmes, les géocaches, et les problèmes à résoudre au quotidien !
Une suggestion ? un problème ? une idée ? Écrire à dCode !
Grille Tournante
Déchiffrement par Grille Tournante
Chiffrement avec une Grille Tournante
Réponses aux Questions (FAQ)
Qu'est ce qu'un chiffrement par grille tournante ? (Définition)
La grille tournante (également connue sous le nom de grille de Fleissner) est une technique de chiffrement par transposition qui consiste à dissimuler un message en disposant ses lettres dans une grille sur laquelle un cache amovible tournant permet de sélectionner les lettres à lire/écrire.
Comment encoder avec une grille tournante ? (Principe de chiffrement)
Pour encoder un message avec une grille tournante, l'utilisateur place une grille perforée ou une feuille comportant des trous par dessus une grille vierge.
Exemple : Chiffrer le message FLEISSNERGRILLE avec la grille
| ▮ | ▮ | ▮ | ▮ |
| ▮ | ▮ | ▯ | ▯ |
| ▮ | ▮ | ▮ | ▯ |
| ▯ | ▮ | ▮ | ▮ |
Les emplacements visibles à travers les trous sont alors remplis avec les lettres du message clair.
Exemple :
| ▮ | ▮ | ▮ | ▮ |
| ▮ | ▮ | F | L |
| ▮ | ▮ | ▮ | E |
| I | ▮ | ▮ | ▮ |
Une fois remplis, la grille trouée est alors tournée d'un quart de tour (sens horaire ou anti-horaire), révélant de nouveaux emplacements libres, qui sont à leur tour remplis des lettres du message clair.
Exemple :
| 1⟳ |
| 2⟳ |
| 3⟳ |
|
Après 4 rotations, la grille est sensée être pleine.
La lecture en ligne de la grille de lettres constitue le message chiffré.
Exemple : Le message est chiffré SLLRGEFLRISEINEG depuis la grille obtenue :
| S | L | L | R |
| G | E | F | L |
| R | I | S | E |
| I | N | E | G |
Si le message contient davantage de lettres, alors recommencer les étapes avec les lettres suivantes et une nouvelle grille vierge (mais en conservant la même grille perforée).
Si la grille n'est pas entièrement remplie, insérer des lettres aléatoires/neutres afin de compléter les trous.
La grille doit respecter certaines règles afin que les trous ne se retrouvent pas sur les mêmes lettres après rotation.
Comment décoder un message avec une grille tournante ? (Principe de déchiffrement)
Pour décoder un message chiffré avec une grille tournante, le joueur place la grille perforée sur le texte codé, alignant les trous avec les caractères.
Les caractères visibles à travers les trous de perforation révèlent les lettres du message original.
Après 4 rotation dans le sens horaire (ou anti-horaire), le message original est entièrement reconstitué.
Si le message contient davantage de lettres, alors recommencer les étapes avec les lettres suivantes.
Comment générer une grille valide ?
La grille doit comporter 1/4 de trous pour 3/4 de non-trous. Puisque les trous occupent successivement 4 positions, seule une de ces positions peut contenir un trou.
Une manière aisée de ne pas avoir de trou dupliqué est de séparer la grille en 4 quadrants, puis de numéroter les cases comme suit : 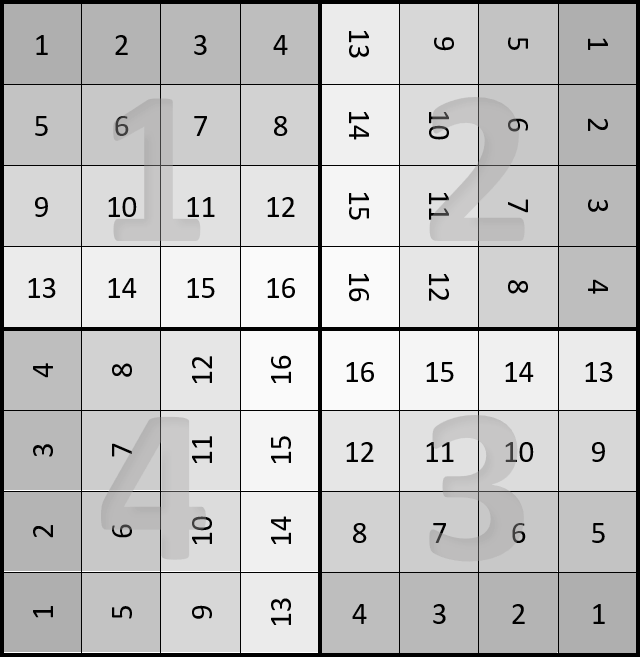
Réaliser des trous pour chaque valeur, mais en se limitant à 1 trou par valeur (à n'importe quel emplacement aléatoire parmi les 4).
Pour les grilles de taille impaire, ne pas tenir compte de la case centrale.
Pourquoi ces grilles s'appellent de Fleissner ?
La méthode des grilles tournantes a été détaillée par le colonel autrichien Edouard Fleissner von Wostrowitz, qui l'a détaillée dans son ouvrage intitulé Handbuch der Kryptographie. Impossible d'affirmer avec certitude qu'il en soit l'inventeur, car des techniques de chiffrement utilisant des grilles existaient depuis longtemps, le nom de Fleissner est resté associé à cette méthode.
Jules Verne, en 1885, a intégré cette technique cryptographique dans son roman Mathias Sandorf, en la créditant à Fleissner.
Ce type de grilles fut utilisé pendantla Première Guerre Mondiale par l'armée allemande. Chaque taille de grille possédait un nom de code : Anna 5x5, Berta 6x6, Clara 7x7, Dora 8x8, Emil 9x9, Franz 10x10.
Comment reconnaitre le chiffre par grille tournante ? (Identification)
Le message chiffré est une transposition des lettres, l'indice de coincidence est similaire à celui du texte clair.
La présence d'une carte perforée (ou tout autre objet similaire) doit faire penser à cette méthode ou au chiffre de Cardan.
Toute référence à Mathias Sandorf ou à Jules Verne est un indice.
Comment déchiffrer sans grille ? (Attaques)
Le déchiffrement d'un message sans avoir la grille correspondante est difficile.
Les attaques potentielles incluent la recherche de motifs récurrents dans le texte chiffré, l'analyse statistique des lettres, mais surtout des méthodes de force-brute. Le nombre de permutation de la grille est relativement limité si sa taille est faible.
Quelles sont les variantes de la grille tournante ?
Il existe plusieurs variantes de la grille tournante, notamment des grilles de tailles différentes ou des méthodes pour tourner la grille selon le sens horaire ou anti-horaire.
Code source
dCode se réserve la propriété du code source pour "Grille Tournante". Tout algorithme pour "Grille Tournante", applet ou snippet ou script (convertisseur, solveur, chiffrement / déchiffrement, encodage / décodage, encryptage / décryptage, traducteur) ou toutes fonctions liées à "Grille Tournante" (calculer, convertir, résoudre, décrypter / encrypter, déchiffrer / chiffrer, décoder / encoder, traduire) codés en langage informatique (Python, Java, C#, PHP, Javascript, Matlab, etc.) ou toute base de données, ou accès API à "Grille Tournante" ou tout autre élément ne sont pas publics (sauf licence open source explicite type Creative Commons). Idem avec le téléchargement pour un usage hors ligne sur PC, mobile, tablette, appli iPhone ou Android.
Rappel : dCode est une ressource éducative et pédagogique, accessible en ligne gratuitement et pour tous.
Citation
Le contenu de la page "Grille Tournante" ainsi que ses résultats peuvent être copiés et réutilisés librement, y compris à des fins commerciales, à condition de mentionner dCode.fr comme source.
L'export des résultats est gratuit et se fait simplement en cliquant sur les icônes d'export ⤓ (format .csv ou .txt) ou ⧉ copier-coller.
Pour citer dCode.fr sur un autre site Internet, utiliser le lien :
Dans un article scientifique ou un livre, la citation bibliographique recommandée est : Grille Tournante sur dCode.fr [site web en ligne], consulté le 16/04/2025,
- Déchiffrement par Grille Tournante
- Chiffrement avec une Grille Tournante
- Qu'est ce qu'un chiffrement par grille tournante ? (Définition)
- Comment encoder avec une grille tournante ? (Principe de chiffrement)
- Comment décoder un message avec une grille tournante ? (Principe de déchiffrement)
- Comment générer une grille valide ?
- Pourquoi ces grilles s'appellent de Fleissner ?
- Comment reconnaitre le chiffre par grille tournante ? (Identification)
- Comment déchiffrer sans grille ? (Attaques)
- Quelles sont les variantes de la grille tournante ?
